Toy Models of Superposition

This paper is part Anthropic’s mechanistic interpretability research. The field of mech interp focuses on reverse engineering neural networks into something understandable/interpretable.

Definitions and Motivation:

Linear representation hypothesis: neural networks represent features of the input as directions in activation space. For example, Mikolov et al. famously found that vector(“King”) - vector(“Man”) + vector(“Woman”) results in a vector close to vector(“Queen”).
- So what are these directions? The vector space of a neural network layer’s activations is called the “representation.” The basis dimensions in this activation space are described as privileged or non-privileged. In a representation where basis dimensions are non-privileged, features can be embedded along any direction (i.e. the basis dimensions are not special). In a representation where the basis dimensions are privileged, features tend to align with those basis dimensions. Privileged basis directions are called “neurons.” (Neurons respond to particular patterns of input, much like how privileged basis directions correspond to particular interpretable features of the input.)
Superposition hypothesis: when neural networks attempt to represent more features than there are neurons, features correspond to almost-orthogonal directions in activation space.
- There exists significant empirical evidence that neurons can be “polysemantic” even when there is a privileged basis. The presence of one feature may cause a slight activation of another feature in activation space, but this interference is the cost of superposition.
- The idea is that a smaller neural network may noisily simulate a larger neural network.

Experiment:

Now, the researchers set out to demonstrate the superposition hypothesis. Let there be an ideal larger model with activation $x \in \mathbb{R}^n$ which perfectly captures all features. The question is whether $x$ can be projected into a lower dimensional vector $h \in \mathbb{R}^m$ then recovered ($x \to x’$), simulating how a non-ideal smaller model might nosily simulate an ideal larger model. This setup can be thought of an autoencoder, and the goal here is interpret the behavior of a simple autoencoder. 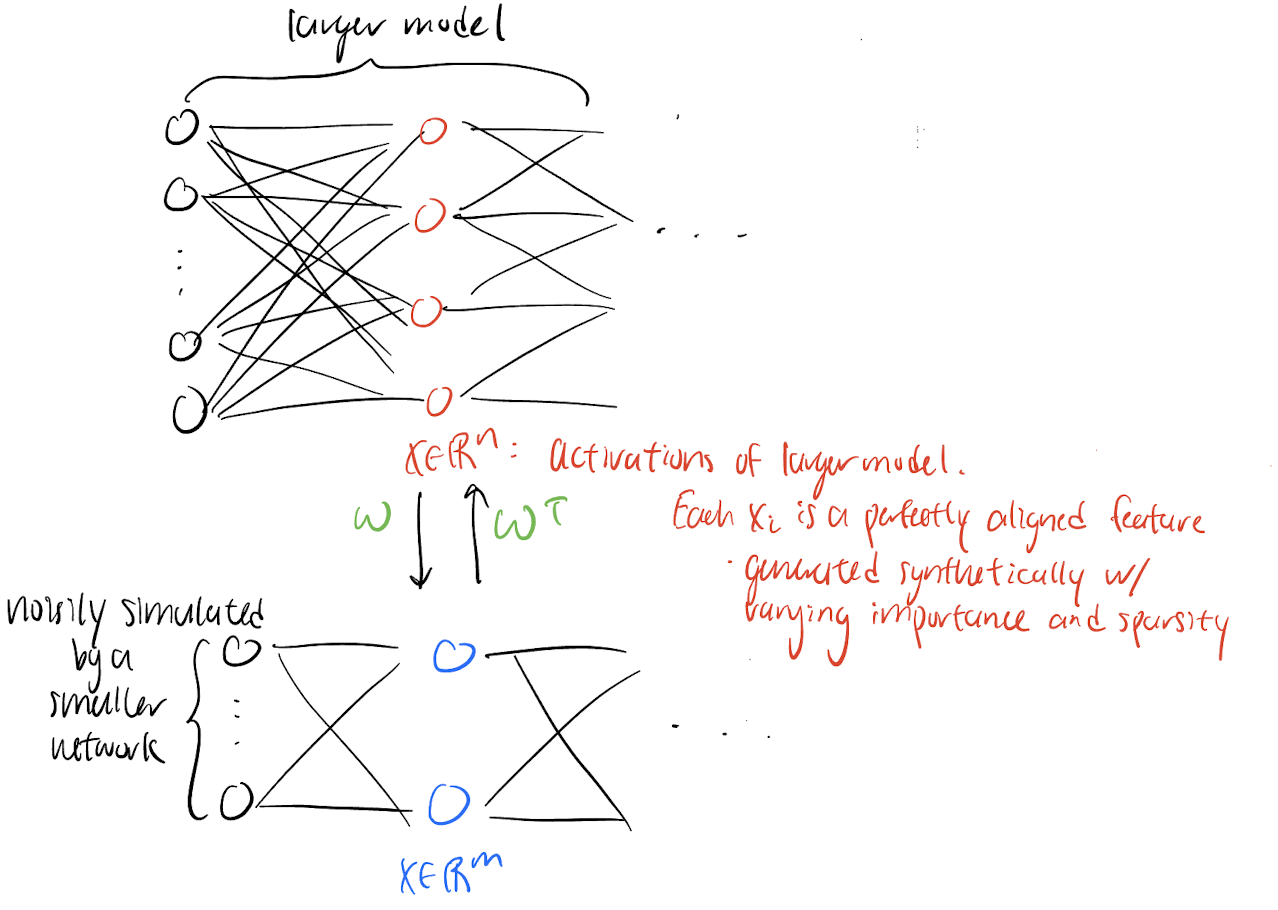Setup Consider two models:

Linear model (no activation): $h = Wx, x’ = W^Th + b$
ReLU model: $h = Wx, x’ = ReLU(W^Th + b)$

Results:

Here $n = 20, m = 5$. That is, there are 20 features of varying importance but the smaller model only has 5 dimensions to work with.
The top row of plots is a visualization of $W^TW$, which is some sort of identity mapping $x \to x’$.
The bottom row of plots represent the magnitude of the column vectors of $W$, which is the norm of the embedding vector for a feature. The color of the bar in the second row of plots measures how much a given feature shares its dimension with other features (calculated using a simple dot product). As you look to the right, sparsity of features is increasing.
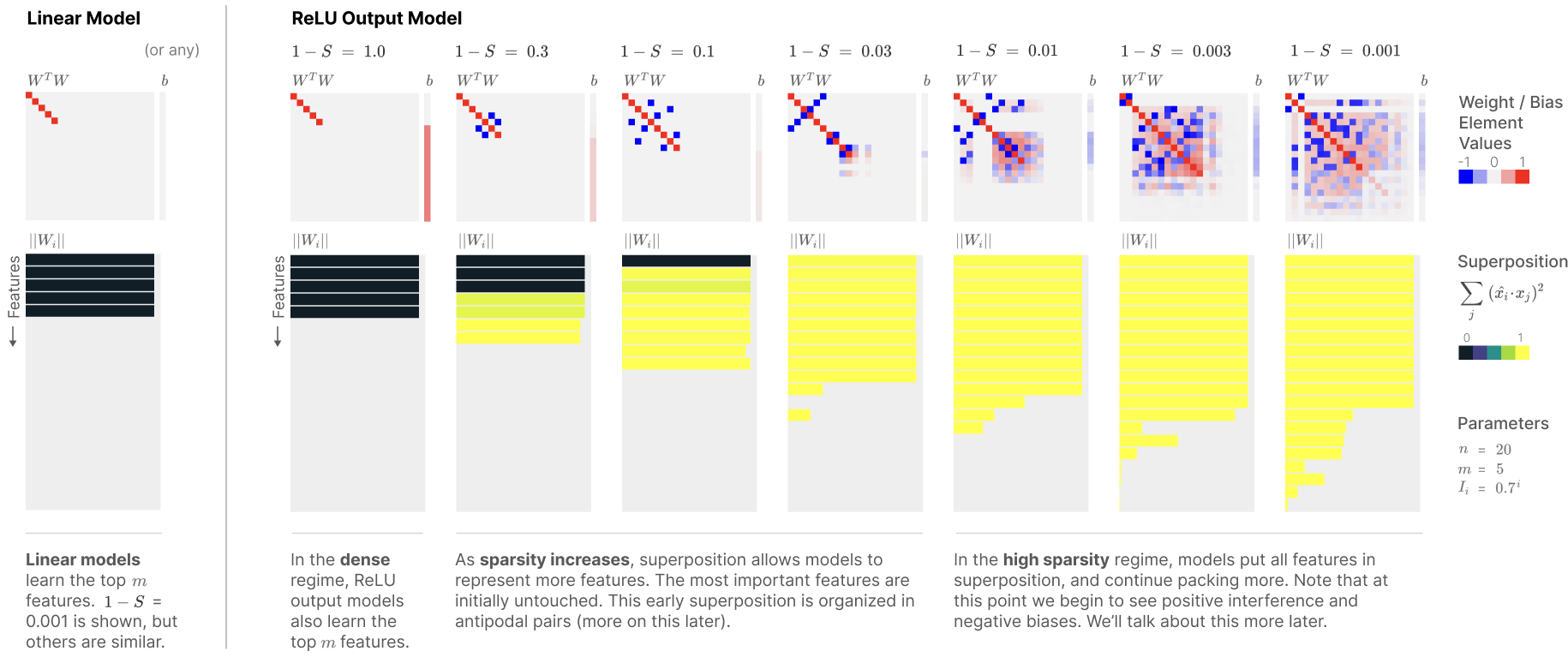
The linear model with no activations represents the top 5 most important features with no superposition.
When there is no sparsity, the ReLU model also learns the top $m$ features.
As sparsity increases, more features are represented using superposition (the embedding vectors of more features becomes nonzero). The least important features are used in superposition, and they are arranged in these sort of opposite pairs.

These are just some of the main points. The paper discusses a lot more than what I have covered.

Bigger picture: To create safe AI, it would be useful to “identify and enumerate over all features.” That is, we want to be able to better understand what types of inputs lead to what types of outputs. Ideally, we would like to know if it is (im)possible to elicit harmful behavior from a model. Better understanding models that do and do not exhibit superposition would be a step in this direction.

Toy Models of Superposition

Mechanistic Interpretability Explainer & Glossary by Neel Nanda